Trong toán học, hàm mũ là hàm số có dạng y = ax, với cơ số a là số dương khác 1.
x, y = x, y = 2x, y = (1/2)x (cơ số ghi ngay trên đồ thị tương ứng).Đồ thị của những hàm số : y = 10, y = e, y = 2, y = ( 50% ) ( cơ số ghi ngay trên đồ thị tương ứng ) .
- Hàm số luôn dương với mọi giá trị của x.
- Nếu a > 1 hàm đồng biến, 0
- Đồ thị nhận trục hoành làm đường tiệm cận và luôn cắt trục tung tại điểm có tung độ bằng 1.
- Đạo hàm:
- d d x e x = e x. { displaystyle , { d over dx } e ^ { x } = e ^ { x }. }
-
d
d
xe
f
(
x
)=
f
′(
x
)e
f
(
x
).
{displaystyle {d over dx}e^{f(x)}=f'(x)e^{f(x)}.}
- d d x a x = a x l n ( a ). { displaystyle , { d over dx } a ^ { x } = a ^ { x } ln ( a ). }
- d d x a x = f ′ ( x ) a f ( x ) l n ( a ). { displaystyle , { d over dx } a ^ { x } = f ‘ ( x ) a ^ { f ( x ) } ln ( a ). }
- Hàm mũ luôn có hàm ngược là hàm logarit.
Các công thức đặc biệt quan trọng[sửa|sửa mã nguồn]
- Từ phép nội suy Taylor người ta tìm được ước lượng như sau:
- e x = ∑ n = 0 ∞ x n n ! = 1 + x + x 2 2 ! + x 3 3 ! + x 4 4 ! + ⋯. { displaystyle e ^ { x } = sum _ { n = 0 } ^ { infty } { x ^ { n } over n ! } = 1 + x + { x ^ { 2 } over 2 ! } + { x ^ { 3 } over 3 ! } + { x ^ { 4 } over 4 ! } + cdots. }
- e x = 1 + x 1 − x x + 2 − 2 x x + 3 − 3 x x + 4 − 4 x x + 5 − 5 x x + 6 − ⋱ { displaystyle , e ^ { x } = 1 + { cfrac { x } { 1 – { cfrac { x } { x + 2 – { cfrac { 2 x } { x + 3 – { cfrac { 3 x } { x + 4 – { cfrac { 4 x } { x + 5 – { cfrac { 5 x } { x + 6 – ddots } } } } } } } } } } } } }
- e 2 x / y = 1 + 2 x y − x + x 2 3 y + x 2 5 y + x 2 7 y + x 2 9 y + x 2 11 y + x 2 13 y + ⋱ { displaystyle e ^ { 2 x / y } = 1 + { cfrac { 2 x } { y-x + { cfrac { x ^ { 2 } } { 3 y + { cfrac { x ^ { 2 } } { 5 y + { cfrac { x ^ { 2 } } { 7 y + { cfrac { x ^ { 2 } } { 9 y + { cfrac { x ^ { 2 } } { 11 y + { cfrac { x ^ { 2 } } { 13 y + ddots , } } } } } } } } } } } } } } }
Trường hợp đặc biệt khi x = y = 1:
- e 2 = 7 + 2 5 + 1 7 + 1 9 + 1 11 + 1 13 + ⋱. { displaystyle e ^ { 2 } = 7 + { cfrac { 2 } { 5 + { cfrac { 1 } { 7 + { cfrac { 1 } { 9 + { cfrac { 1 } { 11 + { cfrac { 1 } { 13 + ddots. } } } } } } } } } } }
Mở rộng cho số mũ phức[sửa|sửa mã nguồn]
x + iy. Hướng từ tối đến sáng theo chiều tăng của trục thực cho thấy hàm số là đơn điệu tăng. Các vạch màu luân phiên tuần hoàn song song với trục thực cho thấy hàm là Đồ thị dạng quang phổ của hàm z = e. Hướng từ tối đến sáng theo chiều tăng của trục thực cho thấy hàm số là đơn điệu tăng. Các vạch màu luân phiên tuần hoàn song song với trục thực cho thấy hàm là hàm tuần hoàn
Người ta đã chứng minh được trong mặt phẳng phức thì công thức ước lượng trên vẫn đúng. Do vậy mọi tính chất của hàm mũ số mũ thực đều đúng trong số mũ phức.
Khi đó, biểu lộ :
- e x + i y = e x × e i y { displaystyle e ^ { x + iy } = e ^ { x } times e ^ { iy } }
Theo công thức Euler ta có:
e
i
y
=
cos
y
+
i
sin
y
{displaystyle e^{iy}=cos y+isin y}
Như vậy:
e
x
+
i
y
=
e
x
(
cos
y
+
i
sin
y
)
{displaystyle e^{x+iy}=e^{x}(cos y+isin y)}
Tuy nhiên cần chú ý quan tâm, phép nâng lũy thừa trong hàm mũ phức không hề giống như mũ thực :
- ( e z ) w ≠ e ( z w ) { displaystyle ( e ^ { z } ) ^ { w } not = e ^ { ( zw ) } }
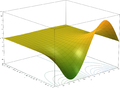Đồ thị hàm Z = Im ( ex + iy ) .
.
Đồ thị hàm Z = Re(ex + iy).
Nếu như cơ số cũng là số phức người ta tính như sau :
- a b = ( r e θ i ) b = e b ( ln r + θ i ) { displaystyle a ^ { b } = left ( re ^ { { theta } i } right ) ^ { b } = e ^ { b ( ln r + { theta } i ) } }
